Ֆլեշմոբային խնդիրների քննարկում ՝ Երկրորդ մակարդակ

Երկրորդ մակարդակ

1. Երկու թվերի գումարը 65 է: Այդ թվերից մեկի և 64-ի գումարը 72 է: Գտեք մյուս թիվը:

{ x+y=65

{ x+64=72

x=72-64

x=8

x+y=65

8+y=65

y=65-8

y=57

(8;57)

Պատ՝․ 57

2. Երեք մետաղադրամիներից մեկը կեղծ է՝ ավելի ծանր է իսկականից, ընդ որում մետաղադրամները արտաքինից իրարից չեն տարբերվում: Նժարավոր կշեռքի օգնությամբ ամենաքիչը քանի՞ կշռումով կարող ես գտնել կեղծը մետաղադրամը:

Ամենաքիչը մեկ անգամ․ Դիտարկենք երկու տարբերակ․

Մենք կարող ենք երկու հատը կշռել,և եթե երկուսն էլ ունենան նույն կշիռները, ապա կեղծը երրորդն է,որը մենք չենք կշռել։ Երկրորդ տարբերակում կարող ենք ունենալ երկու ոչ իրար հավասար։ Այստեղ կեղծը այն է,որը ունի ավելի մեծ կշիռ։

Պատ՝․1

3. Գտեք այն ամենափոքր եռանիշ թիվը, որը բաժանվում է և՛ 3-ի, և՛ 4-ի:

Ամենափոքր եռանիշ թիվը,որը բաժանվում է 3-ի և 4-ի

Դա 108-ն է

108/4=27

108/3=36

Այստեղ մենք օգտվեցինք հայտանիշներից։ Երեքի են բաժանվում այն թվերը,որոնք թվանշանների գումարը բաժանվում է 3-ի։ Իսկ 4-ի են բաժանվում այն թվերը,որոնց վերջին երկու թվանշանները բաժանվում են 4-ի։

Պատ՝․108

4. Մի շարքով պետք է տնկել վեց տնկի՝ 3 խնձորենի և 3 դեղձենի: Նույն մրգի տնկիները իրար նման են, և տարբերվում են մյուս մրգի տնկիներից: Շարքում առաջին և վերջին տնկիները պետք է տարբեր մրգերի լինեն: Քանի՞ տարբեր ձևով է հնարավոր իրականացնել ծառատունկը:

Դիտարկենք այս խնդիրը համարակալելով․

Դեղձերը նշանակենք 1,իսկ խնձորները 2

Մենք չենք կարող առաջին և վերջին մրգերի տեղերը փոխել,ուստի մենք կարող ենք միմիայն փոխել 4 մրգերի տեղեր։

Լինելու ես այսպես․

1,1,1,2,2,2

1,1,2,1,2,2

1,2,2,1,1,2

1,2,1,1,2,2

1,1,2,2,1,2

Քանի,որ մենք կարող ենք տեղերով փոխել առաջին և վերջին մրգերը,դրանով չխախտելով խնդրի պայմանը,որ առաջինը և վերջինը պետք է լինեն տարբեր։ Ուստի մենք կարող ենք տեղերով փոխել և կստանանք նույն պատկերը ինչ առաջինում։ Պատասխանը կլինի

6*2=12

Պատ՝․ 12 տարբերակ

5. Գայանեն գրեց 5, 2, 1, 4 թվանշանները: Նարեն դրանցից ընտրելով 3 թվանշան գրեց 4-ի բաժանվող հնարավոր ամենամեծ եռանիշ թիվը: Եվան այդ նույն թվանշաններից ընտրելով 3 թվանշան, գրեց 4-ի բաժանվող հնարավոր ամենափոքր եռանիշ թիվը: Աղջիկների ընտրած թվանշաններից քանի՞սն են ընդհանուր։

Ամենամեծ թվանշանը այստեղ 5-ն է։ Ուստի եռանիշի առաջին թվանշանը պետք է լինի ամենամեծը հետևյալներից։ 542 չի բաժանվում 4-ի,բայց 524-ը բաժանվում է,ուստի ամենամեծ եռանիշ թիվը այս խնդրում դա 524-ն է,որը բաժանվում է 4-ի։ Իսկ ամենափոքր եռանիշը,որը բաժանվում է 3-ի դա 124-ն է,մենք պարզապես փոխում ենք 5-ի և 1-ի տեղերը,քանի,որ 5-ը ամենամեծն է այստեղ,իսկ 1-ը ամենափոքրը․ Ստացվում է,որ 524-ում և 124-ում ընդհանուր թվանշաններն են 2-ը և 4-ը,ուստի ստացվում է ,որ օգտագործվել է երկու նույն թվանշան։

Պատ․՝ 2 թվանշան

6․ Ավտոմատ սարքում երկու գույնի կոնֆետ կա՝ կարմիր և դեղին: Յուրաքանչյուր 100 դրամի դիմաց սարքը տալիս է մեկ կոնֆետ՝ գույնի ընտրությունը կատարում է պատահականորեն: Արամը ամենաքիչը քանի՞ դրամ պետք է ծախսի, որպեսզի նույն գույնի գոնե երկու կոնֆետ հաստատ ունենա:

Ամենաքիչը մենք պետք է ծախսենք 300 դրամ։ Դիտարկենք երկու տարբերակ․

Եթե մեր առաջին փորձից ընկնի կարմիր կամ դեղին,մենք կարող ենք ասել, որ կունենանք մի գույն,որի երկրորդը չկա։ Երկրորդ փորձից հավանականությունը 1/2- է ,որ կընկնի հենց նույն գույնը։ Ենթադրենք ,որ ընկավ կարմիրը,իսկ մեր մոտ դեղին էր։ Ստացվում է, որ մենք ունեցանք երկու տարբեր գույների կոնֆետ։ Երրորդն էլ կլինի վերջնականը,քանի, որ կապ չունի կընկնի կարմիր,թե դեղին,կարևորը մենք կունենանք մի գույնից երկու հատ։

Պատ՝․ 300 դրամ

7. 15 վարպետը տունը կառուցեցին 150 օրում։ Նույն աշխատանքը 30 վարպետը քանի՞ օրում կավարտեն, եթե բոլոր վարպետները աշխատում են նույն արագությամբ:

Քանի,որ 15 վարպետը կառուցում են 150 օրում,ուստի մի վարպետը կկառուցի ավելի դանդաղ,և դա գտնելու համար մենք 15*150 կանենք,և կստանանք 2250 օր։ Նույն աշխատանքը 30 վարպետը կանի 2250/30=75 օրում։ Նույն տրամաբանությամբ կարող ենք գրել ուրիշ տարբերակով։ Քանի,որ 30-ը 15-ց երկու անգամ մեծ է,ուստի աշխատանքը կկատարվի երկու անգամ ավելի արագ։ Դրա համար մենք պարզապես 150/2 և կստանանք 75,որը նույնպես լուծում է։

Պատ՝․ 75 օրում

8. Ամենաքիչը քանի՞ գույն է անհրաժեշտ 8×8 չափի քառակուսի աղյուսակը ներկելու համար, որ հարևան վանդակների որևէ զույգ նույն գույնի չլինի (վանդակը ամբողջությամբ ներկում ենք մեկ գույնով, հարևան կհամարենք այն վանդակները, որոնք ընդհանուր կողմ ունեն):

Այս խնդիրը նմանացնում է շախմատի տախտակին,որը նույն ձև է կառուցված։ Այնպես,որ երկու նույն գույն չլինեն իրար հարևան։

Այնտեղ էլ է երկու գույնով ներկված,ուստի ամենաքիչը 2 գույնն է,քանի,որ մյուս դեպքերում նույն գույները կլինեն հարևան։

Պատ՝․ 2 գույն

9. Գևորգը geogebra ծրագրում պատկերեց շրջանագիծ և վրան նշեց 15 կետ։ Կետերից յուրաքանչյուրը հատվածով միացրեց նշված կետերից բոլոր մնացածների հետ։ Քանի՞ հատված կստացվի:

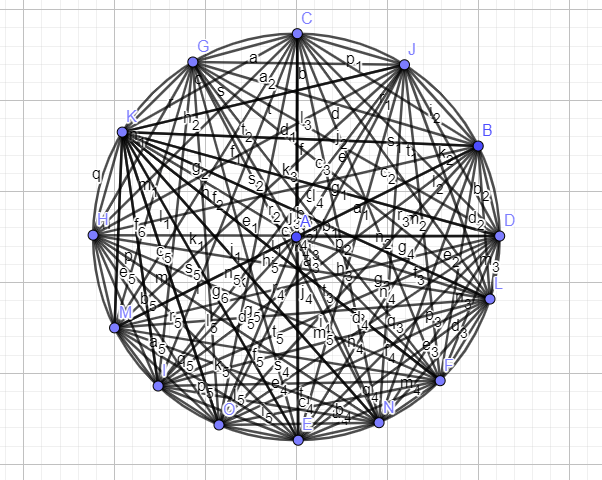
Կստացվի մոտավորապես հետևյալ պատկերը․

Մենք կարող ենք հաշվել հետևյալ ձև։

Քանի,որ առաջին կետից 15 ուղղությամբ տանելու դեպքում կստացվի 15 հատված։ Քանի,որ ամեն հերթափոխից հետո մենք ունենում ենք արդեն երկու կետերով վերցված հատված,ուստի մենք պետք է այն հաշվի չառնենք։ Կստացվի այսպիսի մի լուծում․

15+14+13+12+11+10+9+8+7+6+5+4+3+2+1=120

Պատ՝․ 120 հատված

10. Մաթեմատիկայի օլիմպիադայի ժամանակ Աշոտը պետք է 20 խնդիր լուծեր: Ժամանակը լրանալուց հետո, Աշոտը հաշվեց, որ իր լուծած խնդիրների քանակը չորս անգամ ավելի շատ է, քան չլուծածները: Քանի՞ խնդիր էր լուծել Աշոտը:

Այստեղ նույնպես պետք է հաշվի առնենք 4-ի հայտանիշները։ Այս խնդիրը կարելի է լուծել 20-4 տարբերակով,որը արդյունքում կտա 16 պատասխանը։ Իսկ 16-ը 4 անգամ մեծ է 4-ից։ Այսինքն 4²=16:

Պատ՝․ 16