Անկյան սինուսը, կոսինուսը և տանգենսը

Կոորդինատային հարթության մեջ կառուցենք 1 շառավղով կիսաշրջանագիծ, որի կենտրոնը կոորդինատների սկզբնակետն է: Այն անվանենք միավոր կիսաշրջանագիծ:

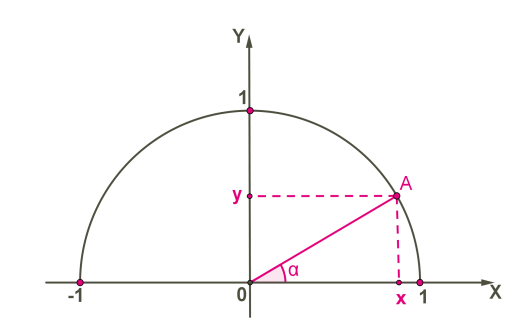
Դիտարկենք α սուր անկյունով AOX ուղղանկյուն եռանկյունը:

Գիտենք, որ սուր անկյան սինուսը հավասար է անկյան դիմացի էջի հարաբերությանը ներքնաձիգին, իսկ կոսինուսը՝ կից էջի հարաբերությանը ներքնաձիգին:

Այսպիսով՝

sin α=AX/AO, cos α=OX/AO,

քանի որ կիսաշրջանագծի շառավիղը R=AO=1, ապա sinα=AX, cosα=OX

0°≤α≤180° միջակայքի ցանկացած α անկյան սինուս կոչվում է A կետի y կոորդինատը, իսկ կոսինուս՝ այդ կետի x կոորդինատը՝ A(cos α;sin α)

Հետևաբար, 0°≤α≤180° միջակայքի ցանկացած անկյան համար տեղի ունեն հետևյալ անհավասարությունները՝ −1≤cos α≤1;0≤sin α≤1

1) α անկյան (α≠90°) տանգենս կոչվում է tg α=sinα/cosα հարաբերությունը:

2) α անկյան (α≠0°,180°) կոտանգենս կոչվում է ctg α=cos α/sin α հարաբերությունը:

Տանգենսի (α≠90°) և կոտանգենսի (α≠0°,180°) արժեքները որոշված չեն նշված անկյունների դեպքում, քանի որ դրանց համար կոտորակների հայտարարները հավասար են զրոյի:

Քանի որ ctg α=1/tg α, ապա կոտանգենսի կիրառությունը փոխարինվում են տանգենսով:

Բերված սահմանումների միջոցով և օգտագործելով միավոր շրջանագիծը, ստանում ենք 0°;90°;180° անկյունների սինուսի, կոսինուսի և տանգենսի արժեքները՝

sin 0°=0, cos 0°=1, tg 0°=0, sin 90°=1, cos 90°=0, tg 90° գոյություն չունի

sin 180°=0, cos 180°= −1, tg 180°=0

Առաջադրանքներ՝