1․ Երեք պահեստ միասին ստացան ինչ-որ քանակի կարտոֆիլ։ Առաջին և երկրորդ պահեստները միասին ստացան 400տ, երկրորդ և երրորդ պահեստները միասին՝ 300տ, իսկ առաջինն ու երրորդը միասին՝ 440տ։ Քանի՞ տոննա կարտոֆիլ ստացավ յուրաքանչյուր պահեստը։
I — x, II — y, III — z
{ x+y=400
{ y+z=300
{ x+z=440
{ y=400-x
{ 400-x+z=300
{ z=440-x
{ y=400-x
{ 400-x+440-x=300
{ z=440-x
{ y=400-x
{ 540=2x
{ z=440-x
{ y=400-x
{ x=270
{ z=440-x
{ y=400-270=130
{ x=270
{ z=440-270=170
Պատ՝․ 270, 130, 170
2. Հեծանվորը 4 օրում անցավ 88կմ։ Ինչքա՞ն ճանապարհ էր անցել առաջին օրը, եթե հայտնի է, որ ամեն հաջորդ օրը նախորդ օրվա համեմատ 2կմ-ով քիչ էր անցել։
Հեծանվորդի՝ առաջին օրվա անցած ճանապարհը նշանակենք x, այնուհետև՝ ըստ օրերի հաջորդականության՝ անցած ճանապարհը պակասելու է՝ x-2, x-4, x-6
x-2+x-4+x-6+x=88
4x-12=88
4x=100
x=25 (առաջին օրը)
x-2=25-2=23 (երկրորդ օրը)
x-4=25-4=21 (երրորդ օրը)
x-6=25-6=19 (վերջին՝ չորրորդ օրը)
Պատ՝․ 25
3․ Միքայելն, Անին և Արշակը միաժամանակ սկսեցին մրցել 100մ երկարություն ունեցող ուղիղ վազքուղով։ Երբ Անին տեղ հասավ, Արշակը նրանից 10մ էր հետ, իսկ երբ Արշակը տեղ հասավ, Միքայելը նրանից 10մ էր հետ։ Քանի մետր էր Միքայելը հետ Անիից, երբ Անին տեղ հասավ։
Պատ՝․ 20 մ
4. Պահանջվում է 33մ երկարությամբ պարանը կտրել այնպեսի երկու մասի, որ կարճ կտորի երկարությունը դեցիմետրերով հավասար լինի երկար կտորի երկարությանը՝ մետրերով։ Գտեք երկար կտորի երկարությունը մետրերով։
Դեցիմետրերը պետք է ավելի քիչ լինեն, այսինքն՝ կարճ մասն ավելի փոքր է։ Նմանատիպ դեպք կարող ենք ունենալ, երբ դեցիմետրերն ու մետրերը 30 են։ 30 դ = 3 մ, հետևաբար՝ երկար կտորի երկարությունը 30 մ է։
Պատ՝․ 30 մ
5․ Գրե՛ք բոլոր այն եռանիշ թվերի քանակը, որոնց միավորների կարգում 6 թվանշանն է, իսկ տասնավորների և հարյուրավորների կարգում գրված թվանշանների գումարը հավասար է միավորների կարգում գրված թվանշանին։
Դիտարկենք ABC ձևով եռանիշ թիվ, որտեղ A-ն հարյուրավոր թվանշանն է, B-ն տասնյակը, իսկ C-ն՝ միավորների թվանշանը:
Պայմանն այն է, որ միավորների թվանշանը 6-ն է, իսկ տասնյակների և հարյուրյակների թվանշանների գումարը հավասար է միավորների թվանշանին։ Այսպիսով, մենք ունենք հետևյալ պայմանները.
C=6 (միավորների թվանշանը 6 է)
A+B=6 (տասնյակների և հարյուրավոր թվերի գումարը հավասար է միավորների թվանշանին)
- Եթե A=1, ապա B=5
- Եթե A=2, ապա B=4
- Եթե A=3, ապա B=3
- Եթե A=4, ապա B=2
- Եթե A=5, ապա B=1
- Եթե A=6, ապա B=0
Նմանատիպ թվեր են 156, 246, 336, 426, 516, 606
Պատ՝․ 6
6․ Երբ հայրս 31 տարեկան էր, ես 8 տարեկան էի, իսկ այժմ նա ինձանից երկու անգամ մեծ է։ Ես այժմ քանի՞ տարեկան եմ։
Երբ հայրը 31 տարեկան էր, որդին 8 էր։ Նրանց միջև տարիքային տարբերությունը 31-8=23 է ու դա անփոփոխ է։ Հիմա հայրը երկու անգամ մեծ է որդուց։
Քանի որ տարիքային տարբերությունը նրանց միջև 23 է, ապա առաջին դեպքը, երբ հայրը որդուց երկու անգամ մեծ կլինի, այն դեպքն է, երբ որդին 23 է, իսկ հայրը՝ 46:
Պատ՝․ 23
7. Մի քանի սովորողներ կանգնեցին շրջանաձև: Պարզվեց, որ յուրաքանչյուր սովորողի հարևանները կա՛մ երկուսն էլ աղջիկ են, կա՛մ երկուսն էլ տղա: Քանի՞ աղջիկ կանգնեց, եթե տղաները 5-ն են:
Պատ՝․ 5 աղջիկ
8. Արամը գումարեց ընթացիք շաբաթվա շաբաթ և կիրակի օրերի ամսաթվերը և ստացավ՝ 27։ Ի՞նչ կստանար Արամը, եթե գումարեր այդ շաբաթվա մնացած օրերի ամսաթվերը։
Ըստ տրամաբանության՝ շաբաթ ամսի 13-ն էր, կիրակի՝ 14-ը։
12+11+10+9+8=20+20+10=50
Պատ՝․ 50
9. Արսենը, Բաբկենը, Գագիկը, Դավիթը, Երվանդը և Զավենը զառ են գցում։ Յուրաքանչյուրի գցած թիվը տարբերվում է մնացածից։ Արսենի թիվը երկու անգամ մեծ Բաբկենի թվից։ Արսենի թիվը երեք անգամ մեծ է Գագիկի թվից։ Դավիթի թիվը չորս անգամ մեծ է Երվանդի թվից։ Ի՞նչ թիվ է գցել Զավենը։
Արսենի թիվը 6-ն է, իսկ Բաբկենինը՝ 3: Քանի որ Արսենի թիվը երեք անգամ մեծ է Գագիկի թվից, ապա վերջինիս թիվը 2-ն է։ Դավիթի թիվը 4-ն է, Երվանդինը՝ 1։ Զավենը գցել է 5-ը։
Պատ՝․ 5
10. Նկարի շրջանակներից երեքում Արամը գրել է 6, 7 և 8 թվերը։ Մնացած շրջանակներում նա պետք է գրի 1, 2, 3, 4 և 5 թվերն այնպես, որ քառակուսու յուրաքանչյուր կողմի վրա գրված թվերի գումարը հավասար լինի 13-ի։ Այդ դեպքում որքա՞ն կլինի մոխրագույն շրջանակներում գրված թվերի գումարը։
8+3+2=13
2+6+5=13
5+7+1=13
1+4+8=13
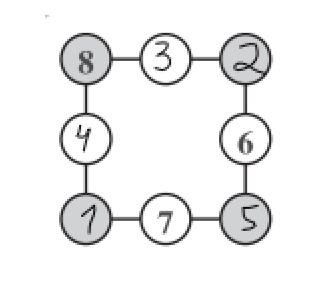
8+2+5+1=16
Պատ՝․ 16
