Թեմա՝ Կրկնակի անկյան եռանկյունաչափական ֆունկցիաների հատկություն դասագիրք՝ առաջադրանք ․138-149
Առաջադրանք 138
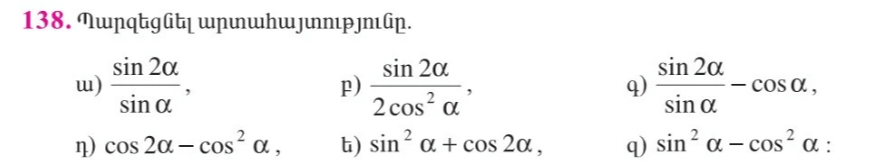
ա) sin2α/sin α=2sin αcos α/sin a=2cos α
բ) sin2α/2cos2α=2sin α/2cos α=sin α/cos α=tg α
գ) sin2α/sin α — cos α=2sin α*cos α/sin α — cos α=2cos α — cos α=cos α
դ) cos2α — cos2a=(2cos2α-1) — cos2α=cos2α-1=cos2α — sin2α — cos2α= -sin2α
ե) sin2α+cos2α=sin2α+1-2sin2α=1-sin2α=cos2α
զ) sin2α-cos2α= -cos2α
Առաջադրանք 139

ա) 2sin π/12*cos π/12=sin2π/12=sin π/6=sin 300=1/2
բ) cos2150-sin2150=2cos*150=cos 300=√3/2
գ) 8sin2π/8*cos2π/8=8*(1-cos450/2 * 1+cos450/2)=2*(1-cos245)=2*(1-2/4)=2* 2/4=1
դ) 2*(sin2π/8-cos2π/8)2=2*(cos2π/8-sin2π/8)2=2*(cos2π/8)2=2*(cos π/4)2=2*(√2/2)2=2* 2/4=4/4=1
Առաջադրանք 140


ա) 2tg 150/1-tg2150=tg2*150=tg 300=√3/3
բ) 2√3*tg 750/1-tg2750=2√3*tg(300+450) / 1-tg(300+450)2=(2√3*(√3/3+1/1-√3/3*1)) / (1-(√3/3+1/1-√3/3*1))2=√3(√3-3) / (-(√3-3)*√3)= -1
գ) ctg23π/8-1/2ctg*3π/8=ctg*2*3π/8=ctg 1350= -1
Առաջադրանք 141

ա) sin2π/8+2sin2π/12=(6-√2/4)-√3/2
բ) cos2π/12-sin2π/8=(√3+√2)/4
գ) 4cos2π/8-6cos2π/12= -1+√2 — (3√3/2)
դ) 2sin2π/12+8cos2π/8=5-√3/2+2√2
Առաջադրանք 149
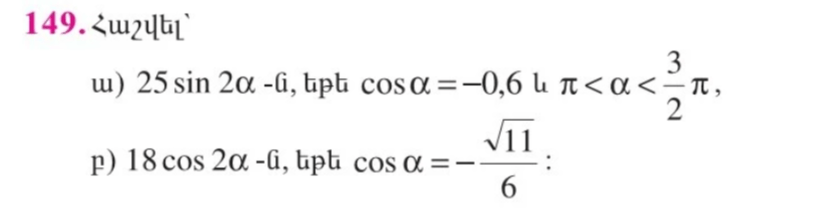
ա) 25sin 2α=24; cos α= -0.6; π<α<3/2π
25sin 2α=25*(2sin α*cos α)=50sin α*cos α
sin2α+cos2α=1
sin2α=1-0.36=0.64
Քանի որ sin-ը III կարգում է, ուստի sin-ը մինուս է => sin=√0.64= -0.8
50sin α*cos α=50*(-0.8)*(-0.6)=24
բ) 18cos2α= -7; cos α= -√11/6
18cos2α=2cos2α-1
18*(2cos2α-1)=18*(2*(11/36)-1)=36*11/36-18=11-18= -7
