Աստիճանային ֆունկցիա. առաջադրանքներ

Աստիճանային ֆունկցիա կոչվում է f(x)=x^a բանաձևով տրված ֆունկցիան, որտեղ a-ն զրոյից տարբեր որևէ թիվ է։

Բնական ցուցիչով աստիճանային ֆունկցիան իր շատ հատկություններով նման է գծային ֆունկցիային, երբ n-կենտ է, և քառակուսային ֆունկցիային, երբ n-ը զույգ է:

Առաջադրանքներ

1) Դիցուք f(x)=x²⁶։ Բաղդատել թվերը։

ա) f(7) & f(8)
f(7)=7²⁶
f(8)=8²⁶
x ∈ [0; +∞) f↑ => 7 < 8=> 7²⁶ < 8²⁶

գ) f(-24) & f(-23)
f(-24)= (-24)²⁶
f(-23)= (-23)²⁶
x ∈ (-∞; 0] f↓ => (-24) < (-23) => (-24)²⁶ > (-23)²⁶

2) Դիցուք f(x)=x³¹։ Բաղդատել թվերը։

ա) f(13) & f(12)
f(13)=13³¹
f(12)=12³¹
x ∈ [0; +∞) f↓ => 13 > 12 => 13³¹ > 12³¹

գ) f(-4) & f(-10)
f(-4)=(-4)³¹
f(-10)=(-10)³¹
x ∈ (-∞; 0] f↓ => (-4) > (-10) => (-4)³¹ > (-10)³¹

3) Հետևյալ թվերը դասավորեք աճման կարգով.

ա) (3,4)²; (3,4)⁵; (3,4)³

Աճման կարգով — (3,4)²; (3,4)³; (3,4)⁵

գ) (2/5)⁴; (2/5)⁷; (2/5)⁵

Աճման կարգով — (2/5)⁷; (2/5)⁵; (2/5)⁴

4) Կառուցել ֆունկցիայի գրաֆիկը և նշել մոնոտոնության ու նշանապահպանման միջակայքերը։

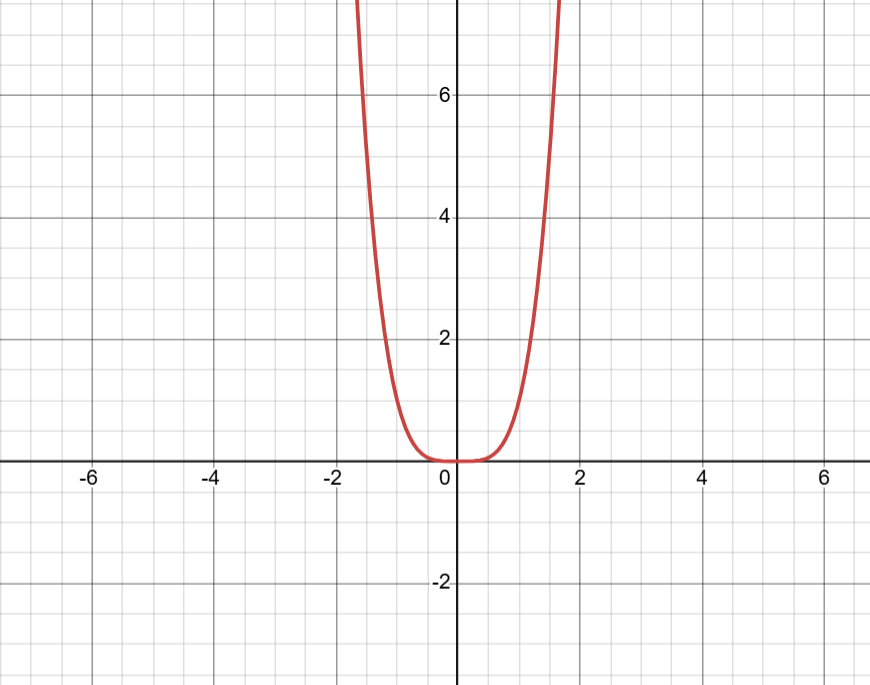
ա) f(x)=x⁴
f(x)=4x³ — ֆունկցիայի I ածանցյալ
f(x)=0, եթե x=0
x > 0 => f(x) > 0 (f↑)
x < 0 => f(x) < 0 (f↓)
Նվազման միջակայք — (-∞; 0)
Աճման միջակայք — (0; +∞)
f(x)=x⁴ միշտ դրական է (x≠0)
Դրական — (-∞; 0) ∪ (0; +∞)

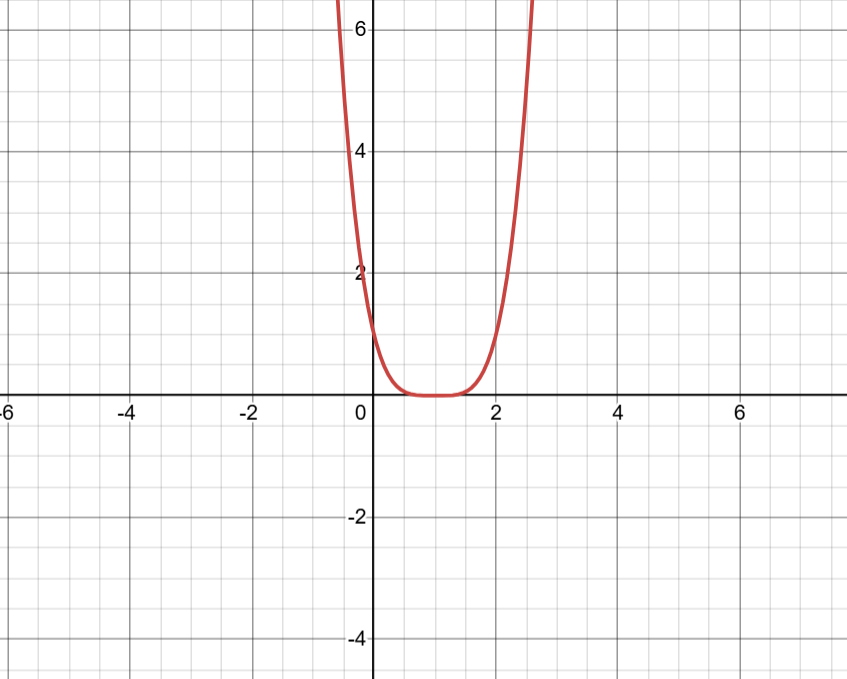
գ) f(x)=(x-1)⁴
f(x)=4(x-1)³ — ֆունկցիայի I ածանցյալ
x > 1 => f(x) > 0 (f↑)
x < 1 => f(x) < 0 (f↓)
Նվազման միջակայք — (-∞; 1)
Աճման միջակայք — (1; +∞)
f(x)=(x-1)⁴ դրական է միշտ
Դրական — (-∞; 1) ∪ (1; +∞)
f(x)=0, եթե x=1