11․ Կրկնության հարցեր

1. Ի՞նչն է կոչվում երկու հատվածների հարաբերություն։

Երկու հատվածների հարաբերություն է կոչվում նրանց երկարությունների հարաբերությունը։

2. Ո՞ր դեպքում են ասում, որ AB և CD հատվածները համեմատական են A₁B₁ և C₁D₁ հատվածներին։

Եթե AB և CD հատվածների հարաբերությունը հավասար է A₁B₁ և C₁D₁ հատվածների հարաբերությանը, այսինքն՝  AB/CD=A₁B₁/C₁D₁, ապա այդ հատվածները կոչվում են համեմատական:

3. Սահմանեք նման եռանկյունները։

Երկու եռանկյուններ կոչվում են նման, եթե նրանց անկյունները համապատասխանաբար հավասար են, և եռանկյուններից մեկի կողմերը համեմատական են մյուսի համապատասխան կողմերին:

4. Բացատրեք, թե ինչ է նմանության գործակիցը։

Նմանության գործակից (k) է կոչվում երկու նման եռանկյունների համապատասխան կողմերի հարաբերությունը։

5. Վերհիշեք և ապացուցեք հավասար անկյուն ունեցող եռանկյունների մակերեսների հարաբերության մասին թեորեմը։

Երկու նման եռանկյունների մակերեսների հարաբերությունը հավասար է նմանության գործակցի քառակուսուն։

Եթե ΔABC∼ΔDEF, ապա S₁/S₂=k²

6․ Ձևակերպեք և ապացուցեք եռանկյունների նմանության առաջին հայտանիշը։

Եթե մի եռանկյան երկու անկյունները համապատասխանաբար հավասար են եռանկյան երկու անկյուններին, ապա այդպիսի եռանկյունները նման են։

Եթե ∢B=∢E և ∢C=∢F, ապա ΔABC∼ΔDEF

7․ Ձևակերպեք և ապացուցեք եռանկյունների նմանության երկրորդ հայտանիշը։

Եթե մի եռանկյան երկու կողմերը համեմատական են մյուս եռանկյան երկու կողմերին, իսկ այդ կողմերով կազմված անկյունները հավասար են, ապա այդպիսի եռանկյունները նման են։

Եթե AB/DE=AC/DF և ∢A=∢D, ապա ΔABC∼ΔDEF

8․ Ձևակերպեք և ապացուցեք եռանկյունների նմանության երրորդ հայտանիշը։

Եթե մի եռանկյան երեք կողմերը համեմատական են մյուս եռանկյան երեք կողմերին, ապա այդպիսի եռանկյունները նման են։

Եթե AB/DE=BC/EF=AC/DF, ապա ΔABC∼ΔDEF

9. Ձևակերպեք և երկու եղանակով ապացուցեք եռանկյան միջին գծի մասին թեորեմը։

Եռանկյան միջին գիծը զուգահեռ է նրա կողմերից մեկին և հավասար այդ կողմի կեսին:

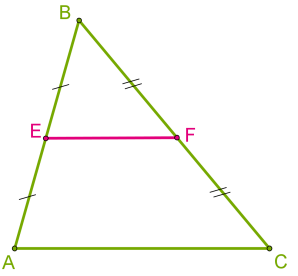
EF ∥ AC; EF=AC/2

10. Ապացուցեք, որ եռանկյան միջնագծերը հատման կետով տրոհվում են 2:1 հարաբերությամբ՝ հաշված գագաթից։

Բոլոր երեք միջնագծերը հատվում են նույն կետում, որը կոչվում է եռանկյան ծանրության կենտրոն, և այդ կետով կիսվում են երկու մասի 2:1 հարաբերությամբ (հաշված գագաթից)։

11. Ձևակերպեք և ապացուցեք պնդումը նման եռանկյունների պարագծերի հարաբերության մասին։

Երկու նման եռանկյունների պարագծերի հարաբերությունը հավասար է նմանության գործակցին: Եթե ΔABC∼ΔDEF , ապա P_ABC/P_DEF=k

12. Ձևակերպեք և ապացուցեք պնդումներ նման եռանկյունների՝ ա) բարձրությունների, բ) միջնագծերի, գ) կիսորդների հարաբերության մասին։

ա) Ուղղանկյուն եռանկյան ուղիղ անկյան գագաթից տարված բարձրությունը համեմատական միջին է այն երկու հատվածների, որոնց տրոհվում է ներքնաձիգը այդ բարձրության հետ հատվելիս։

Եթե  ΔABC∼ΔCBD => AD/CD=CD/DB=> CD²=AD*DB, այսինքն՝ CD=√AD*DB

Ուղղանկյուն եռանկյան էջը համեմատական միջին է ներքնաձիգի և նրա այն հատվածի, որը գտնվում է տվյալ էջի և ուղիղ անկյան գագաթից տարված բարձրության միջև։

Եթե ΔADC∼ΔACD=> AB/AC=AC/AD=> AC²=AB*AD=> AC=√AB*AD

բ) Եռանկյան միջնագծերը հատվում են մի կետում և այդ կետով տրոհվում 2:1 հարաբերությմաբ՝ հաշված գագաթից։

Դիտարկենք կամայական ABC եռանկյուն։ O տառով նշանակենք AA₁ BB₁ միջնագծերի հատման կետը և տանենք A₁B₁ միջին գիծը։ Քանի որ A₁B₁-ը զուգահեռ է AB կողմին, ուրեմն ∢1=∢2 & ∢3=∢4: Հետևաբար՝ AOB & A₁OB₁ եռանկյունները, ըստ երկու անկյան, նման են։ Դա նշանակում է, որ այդ եռանկյունների կողմերը համեմատական են․

AO/A₁O=BO/B₁O=AB/A₁B₁=k

Բայց, քանի որ AB=2A₁B₁, ապա AO=2A₁O & BO=2B₁O: Այսպիսով` AA₁ & BB₁ միջնագծերից յուրաքանչյուրը հատման O կետով տրոհվում է 2:1 հարաբերությամբ՝ հաշված գագաթից։

գ) Եռանկյան անկյան կիսորդը հանդիպակաց կողմը տրոհում է երկու հատվածի, որոնք համեմատական են կից կողմերին։

AD-ն ABC եռանկյան կիսորդ է։ ABD & ACD եռանկյուններն ունեն ընդհանուր բարձրություն՝ AH-ը։ Ուստի` S_ABD/S_ACD=BD/DC։ Մյուս կողմից՝ այդ նույն եռանկյուններն ունեն մեկական հավասար անկյուններ (∢1=∢2): Ուստի՝ S_ABD/S_ACD=AB*AD/AC*AD=AB/AC:

Իսկ մակերեսների հարաբերության այդ երկու հավասարությւոնից ստացվում է․ BD/DC=AB/AC; BD/AB=DC/AC

13․ Բացատրեք, թե որ պատկերներն են կոչվում նման։ Նկարագրեք կենտրոնային նման պատկերների օրինակներ։

Միևնույն ձև ունեցող պատկերները՝ անկախ չափերից, կոչվում են նման։